GPT-4 根本不会推理！

近来，有两篇研究称，GPT-4 在推理方面表现不尽人意。

来自 MIT 的校友 Konstantine Arkoudas，在 21 种不同类型推理集中，对 GPT-4 进行了评估。然后，对 GPT-4 在这些问题上的表现进行了详细的定性分析。

研究发现，GPT-4 偶尔会展现出「最强大脑」的天赋，但目前来看，GPT-4 完全不具备推理能力。

论文地址：https://www.preprints.org/manuscript/202308.0148/v2

研究一出，引来众多网友围观。

马库斯表示，「如果这是真的 —— 正如我早就说过的那样 —— 我们离 AGI 还差得远呢。我们可能需要进行大量的重新校准：没有推理就不可能有 AGI」。

在这个简短的输出中，出现大量惊吓下巴的错误。

GPT-4 一开始就谎称图形是完全的（显然不是，例如顶点 2 和 3 之间没有边）。

此外，显而易见的是，如果图形真是完全的，那么就不可能用 2 种颜色来着色，因为一个有 6 个顶点的完全图形至少需要 6 种颜色。

换句话说，GPT-4 的说法不仅是错误的，而且是前后矛盾的：一会儿告诉我们（错误）这 6 顶点图形是完全的，这意味着不可能用 2 种颜色给它着色，一会儿又提供了一种双色「解决方案」。

值得注意的是，GPT-4 之所以表现如此糟糕，并不是因为它没有掌握足够的图形知识或数据。

当研究人员要求 GPT-4 对「完全图」的了解时，它滔滔不绝地说出了「完全图」的正确定义，以及一长串关于 K_n（有 n 个顶点的完全图）的结果。

显然，GPT-4 已经记住了所有这些信息，但却无法在新条件中应用。

S = {2, 8, 6, 32, 22, 44, 28, 12, 18, 10, 14}。那么 S 有多少个子集的总和是 37？

这个问题中，S 的子集都是偶数，而偶数之和不可能是奇数，因此答案为 0。

然而，GPT-4 没有停下来考虑 S 包含的内容，而是反射性地生成它认为对这个问题合适的答案，然后继续「幻化」出一个答案「4」。

告诉 GPT-4 A × B 代表集合 A 和 B 的笛卡尔积、从 A 到 B 的关系 R 是 A × B 的子集，以及 & 代表集合交集之后要求它证明或证伪：

其中 R1 和 R2 是从 A 到 B 的二元关系，dom (R) 表示二元关系 R 的域。

需要子集关系在 (2) 的两个方向上都成立，但它只在从左到右的方向上成立。另一个方向的反例很容易找到（例如，取 A = {(1, 2)} 和 B = {(1,3)}）。

然而，GPT-4 却推断这是成立的，显然不正确。

罗素理发师悖论是指，存在一个理发师 b，他为且仅为那些不给自己刮胡子的人刮胡子。

这句话的否定是一个同义反复，很容易用一阶逻辑推导出来。

如果我们把 R (a,b) 理解为 a 被 b 刮胡子，那么我们就可以提出这个同义反复，并要求 GPT-4 证明或反证它，如下面 prompt 所示：

如果存在这样一个理发师 x，那么对于所有 y，我们将有 R (y,x) ∼ R (y,y)，因此用 x 代替 y 将得到 R (x，x) ∼ R (x,x)，这是矛盾的。

GPT-4 对所给句子的结构和需要做的事情的理解无可挑剔。然而，随后的案例分析却糊里糊涂。

有五个积木从上往下堆叠：

1. 从上往下数第二个积木是绿色的

2. 从上往下数第四个积木不是绿色的

在这些条件成立的情况下，证伪或证明以下结论：在一个非绿色积木的正上方，有一个绿色积木。

首先它在证明猜想时，就已经弄错了证明的策略 ——PT-4 假定了两种特殊情况来进行推理。

此外，GPT-4 在自己的推理中已经得出了结论（虽然是错的），但在回答时仍然告诉用户问题没有被解决。而这体现的便是模型的内部不一致性问题。

GPT-4 第一次给出的答案是右边，但作者指出了它的错误，虽然从地图上来看，位于马萨诸塞州的波士顿的确在南达科他州的右边，但这里还有一个附加条件：身体的朝向是得克萨斯州。

1. 住在 Dreadbury Mansion 的某人杀了 Agatha 姨妈。

2. Dreadbury Mansion 中唯一的居住者是 Agatha 姨妈、管家和 Charles。

3. 杀人犯总是讨厌他的受害者，并且他的财富不会比受害者多。

4. Charles 不讨厌 Agatha 姨妈讨厌的人。

5. Agatha 姨妈讨厌所有人，除了管家。

6. 管家讨厌所有不比 Agatha 姨妈富有的人。

7. 管家讨厌 Agatha 姨妈讨厌的所有人。

8. 没有人讨厌所有人。

9. Agatha 姨妈不是管家。

正确的答案是 Agatha 姨妈杀了自己。

首先，根据条件 5，Agatha 姨妈必须讨厌她自己，因为她讨厌所有除了管家以外的人。

因此，根据条件 4，得出 Charles 不讨厌她，所以他不可能杀了她。

根据条件 5 和 7，管家不可能讨厌他自己，因为如果他讨厌自己的话，条件 8 就不成立了，他会讨厌所有人。

根据条件 6，得出管家比 Agatha 姨妈更富有，否则他会讨厌自己，这与前面我们得出的他不讨厌自己相矛盾。

根据条件 3，管家也不会是凶手（第 3 个条件）。

沃森选择任务是心理推理领域中的基本内容。

在一月份的论文中，GPT-3.5 就未能通过这个测试，本次研究中，GPT-4 的表现依旧不理想。

这些回答显示，GPT-4 不理解条件语句的语义。当 GPT-4 说卡片「50」和「30」必须翻开时，它似乎将条件误认为是充分必要条件。

而无论 GPT-4 的回答是对还是错，其内部的说法都是不一致的。

信息论的一个基本结论是：随机向量 Z 的熵上界不超过组成 Z 的随机变量的熵之和。

因此，下面问题的答案应该是「在任何情况下都不会」。

最后给 GPT-4 的推理问题是最具挑战性的：证明一个简单表达式编译器的正确性。

这可能是因为它之前看过类似的证明，作者给出的例子是编程课程和教材中常见的练习类型。

然而，GPT-4 还是会出现一些细节上错误。

错误标记为红色，更正内容为紫色

对此，研究中引入了一个大学水平的科学问题基准 SCIBENCH。

其中，「开放数据集」包括从大学课程广泛使用的教科书中收集的 5 个问题，涵盖了基础物理、热力学、经典力学、量子化学、物理化学、微积分、统计学和微分方程。

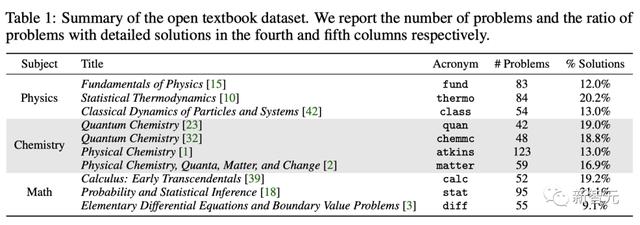
开放数据集中准确率的结果

在使用 CoT 提示 外部工具最强配置下，GPT-4 在开放式数据集上取得了 35.80% 的平均分，在封闭数据集上取得了 51.57% 的平均分。

这些结果表明，在未来的 LLM 中，GPT-4 有相当大的改进潜力。

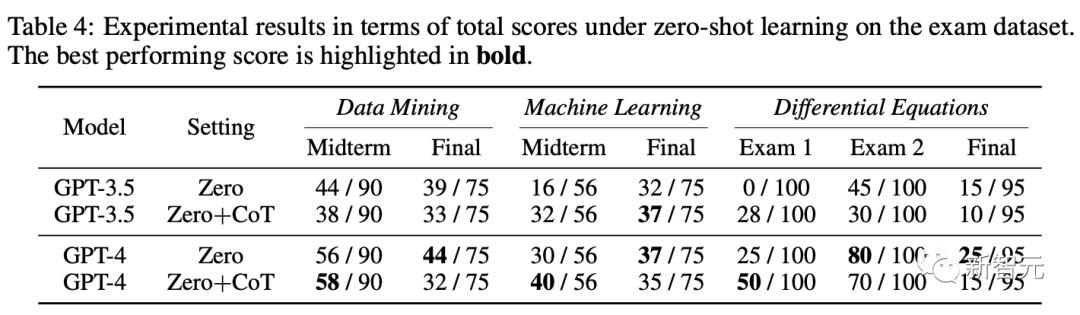
考试数据集上零样本学习下总分的实验结果

为了全面了解 LLM 在科学问题解决中的局限性，研究人员提出了一种全新的「自我完善」的方法，以发现 LLM 所做解答中的不足之处。

便是如下的「评估协议」。

首先，将正确的解决方案与 LLM 生成的解决方案进行比较，并在人工标注员的协助下，总结出成功解决科学问题所需的 10 项基本技能。

具体包括：逻辑分解和分析能力；识别假设；空间感知；因果推理；问题演绎；抽象推理；科学素养；代码转换；逻辑推理；计算能力。

随后，团队采用了一种由 LLM 驱动的自我评价方法，对每个实验配置下基准 LLM 所做的解决方案中，缺乏的技能进行自动分类。

6 种设置下 GPT-3.5 在文本数据集上的错误概况，揭示了其 10 种基本解决问题能力的缺陷分布

最后，通过分析发现：

总之，研究结果表明，当前大型语言模型在解决问题能力方面依旧很弱，并且在各种工具帮助下，依旧存在局限性。